Divide and Conquer

Wednesday, May 13, 2015

8:40 AM

<<divide-and-conquer-2.pdf>>

Inserted from: <file://\\psf\Dropbox\Schoolworks\Waterloo\4B\CS431\divide-and-conquer-2.pdf>

Machine generated alternative text: DM-æd-Capin ‘“[VT’ Racu,,enct ReIaton
Guess-and-check Method
step 1 Tabulate some values a1.a-.. . using the recurrence
relation.
step 2 Guess that the solution a has a specific form, involving
undetermined constants.
step 3 Use to determine specific values for the
unspecified constants.
step 4 Use induction to prove your guess for a is correct.
Wine,, 2015 53/80
— Recr.ence ReIatan
txample ot the Guess-and-check Method
Suppose we have the recurrence T(ri) = T(n — 1) 6n — 5, T(O) = 4.
We compute a few values: T(1) = 5, T(2) = 12, T(3) = 25, T(4) = 44.
If we are sufficiently perspicacious, we might guess that T(rz) is a
quadratic function, e.g, T(rz) = an2 ± 1m ± c.
Next, we use T(O) = 4, T(l) = 5, T(2) = 12 to compute a, b and c by
solving three equations in three unknowns.
We get a = 3, b = —2, c = 4.
Now we can use induction to prove that T(n) = 3n2 2n+4 for all ra O.
D.R. SUman (SCS)
Wines, 2015 54/90

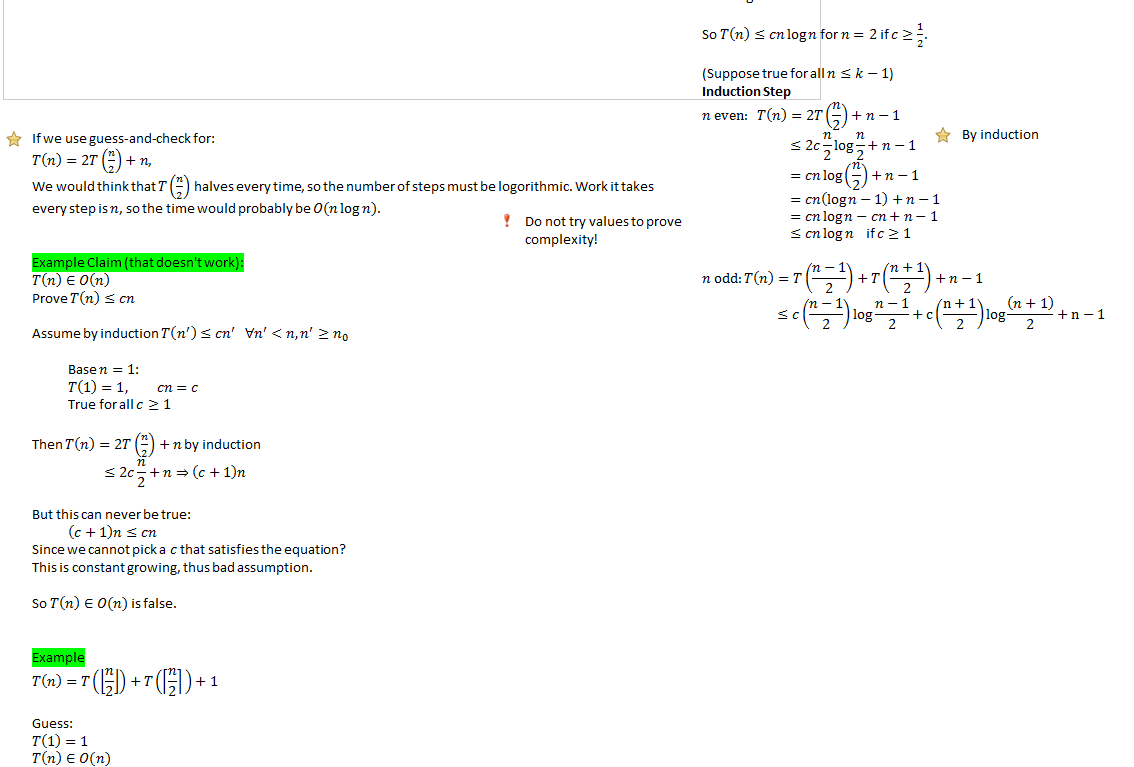
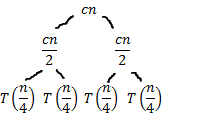
So is the guess wrong?

No, but sometimes the math just doesn't work out.


…
		The floor and ceiling goes away since the result is always an integer

	EX:


			This is unintuitive. We make the induction work by lowering the bound. Read 4.3 from text

Recall Math239 solution of recurrence relations (Homogeneous linear recurrences):


	Master Theorem

Machine generated alternative text: Dêwkfreid-Ca.in AlgiwthJ DiJóe-and-Conqucr Destin Stratcgy
The Divide-and-Conquer Design Strategy
divide: Given a problem instance I, construct one or more smaller
problem instances, denoted Ii.... . 4 (these are called subproblems).
Usually, we want the size of these subproblems to be small compared to
the size of I, e.g., half the size.
conquer: For 1 j a. solve instance 4 recursively, obtaining solutions
Si Sa.
combine: Given Si.. .. . Sg, use an appropriate combining function to
find the solution S to the problem instance I, i.e.,
S *— combine(St. .... Sa).
- °“ (C) Wtnti,, 2015 61180
Mer
txampie: Uesign of Mergesort
Here, a problem instance consists of an array .4 of n integers, which we
want to sort in increasing order. The size of the problem instance is n.
divide: Split .4 into two subarrays: .4. consists of the first [] elements
in A and AR consists of the last [9J elements in A.
conquer: Run Mergesort on A1 and AR.
combine: After A1 and A have been sorted, use a function Merge to
merge A1 and A into a single sorted array. Recall that this can be done
in time 9(n) with a single pass through Ar and -4R We simply keep
track of the “current” element of A1 and AR, always copying the smaller
one into the sorted array.
D.R. SUman (SCS) CS 341
Winter, 2015 62 / 80

Machine generated alternative text: — Mernsart
M ergesort
Algorithm: Mergesart(A: array: n: integer)
il n = 1
then S — A
nL4— F1
flaC [j
AL e [A[1].. . .A[nL]]
else Aa e [A[nL ± 1]... ,4tT1H
5L - Mergesort(AL,nL)
5a — Mergesort(Aa. na)
S e Merge(SL,nz.SR.nR)
return (S, n)
() Wine,, 2015 63/99
r rw—w Mereesort
Analysis of Mergesort
Let T(n) denote the time to run Mergesort on an array of length n.
divide takes time 9(n)
conquer takes time T(F]) —T([j)
combine takes time 9(n)
Recurrence relation:
r(fl)=1T(F1)_T(Li)±9(n) ifn>1
19(1) ifn=1.
D.R. SUman (SCS)
Wntes, 2015 Ut 99

Machine generated alternative text: DMrk-aid-Cier DiJóe-and-Conqucw Recun’cnce Rdathns
Sloppy and Exact Recurrence Relations
It is simpler to replace the O(n) term by cri, where c is an unspecified
constant. The resulting recurrence relation is called the exact recurrence.
ifn>1
P’
If we then remove the floors and ceilings, we obtain the so-called
sloppy recurrence:
T(n_f2T±01 ifn>1
P’
The exact and sloppy recurrences are identical when n is a power of two.
Further, the sloppy recurrence makes sense only when n is a power of two.
DR. 5dm,,. (SCS) CS 241 Winter, 2015 65 ,‘ 90
fl’’7rT-! Dhlde-and-Conquct Recurnnce Rdatlanz
Lomplexity of the Solution to the Exact Recurrence
The Master Theorem provides the exact solution of the recurrence when
n = 2 (it is in fact a proof for these values of n).
We can express this solution (for powers of 2) as a function of n, using
6-notation.
It can be shown that the resulting function of n will in fact yield the
complexity of the solution of the exact recurrence for all values of n.
This derivation of the complexity of T(n) is not a proof, however. If a
rigourous mathematical proof is required, then it is necessary to use
induction along with the exact recurrence.
D.t SUma. (SS)
Winte., 2015 66 / 90

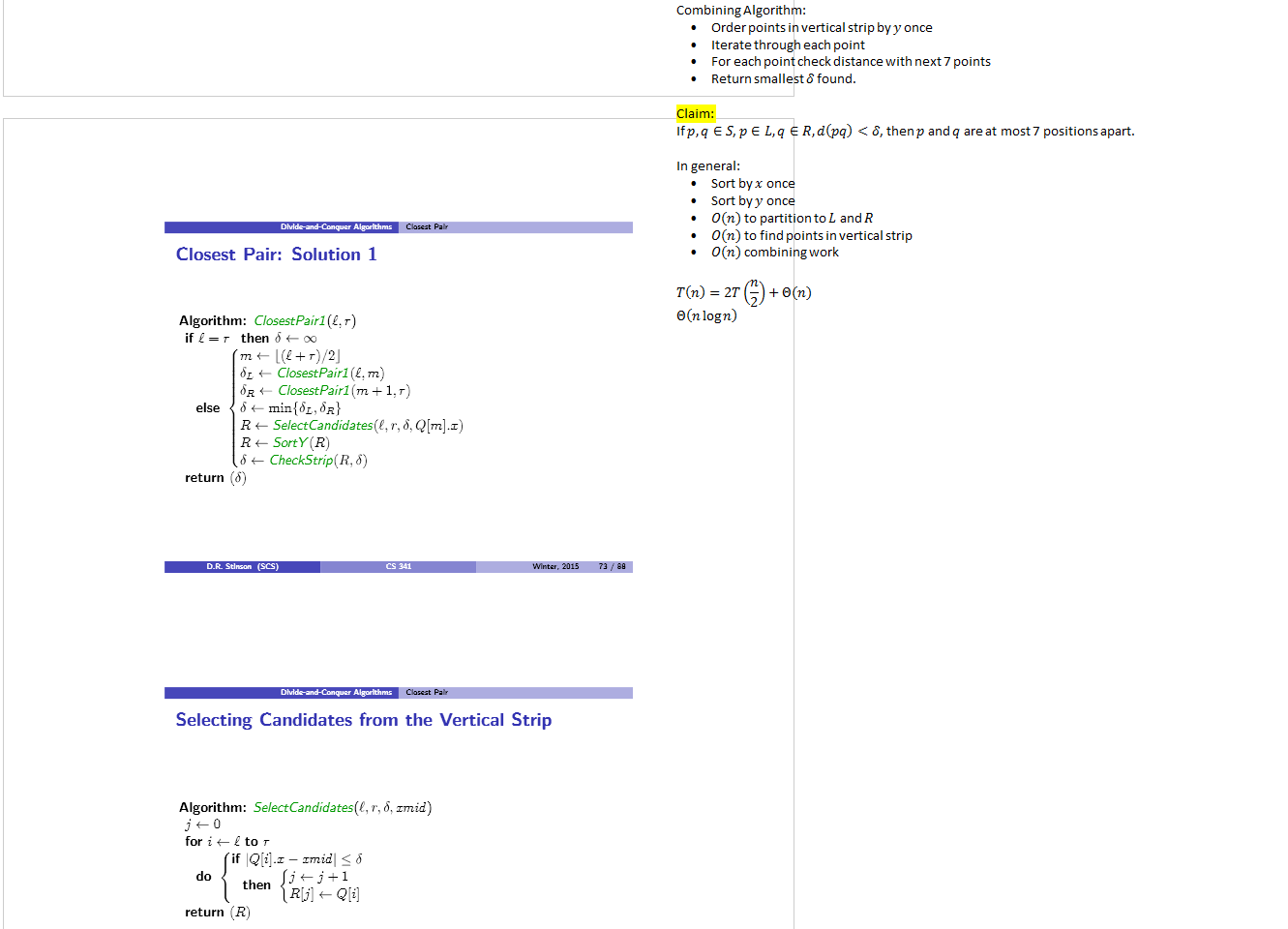
$Machine generated alternative text: DMik-atd-Ca.iai Algw*I,sJ CL2scst Pair Checking the Vertical Strip Algorithm: checkstrip(R. 6) t t- size(R) 6’ — ¿ [or j <— 1 to t — 1 [or k t— j—1 to rnin{t.j + 7) -r t— R[j]r z’*— R[k].x do do yt-RjJ.y y’ t— R[kJy ________________ o’ €— rnin{o’. \/(Y — ± (y’ — y)2} return (å) Dk Sd.a. (fl —‚ Clascat PaW Llosest Pair: Solution 2 Algorithm: CïosestPair2(L. r) i[i=r then 6foc mt— (t+r)/2j & .— ClosestPair2(L m) comment: -- - Q] ¡s sorted WRT y-coordinates 6 t- CiosestPair2(m ± 1. r) else comment: Qm ± 1]. . . . Q[rJ ¡s sorted WRT y-coordinates 6 *— min{ÕL, ÒR} MergeÇë. m. r) R t— SeÍectCandidates(t, r, ¿. Q[m]x) ¿ 4— CheckStrip(R,ó) return (à) I Wine,, 2015 75/80 Wines, 2015 76 ,,‘ 90 Dt SUman (SCS)$